A Little Bit of Magic

Hi everyone! It's Lu again, back with another update.

Today, I'm going to talk a little about a piece of mathematical "magic."
Ladies and gentlemen, let me introduce...the 3x3 magic square.

Magic square of order 3.

Take a close look. What do each of the rows add up to? What about the columns? And the diagonals? They all add to 15! How magical.

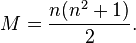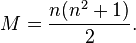An n-by-n magic square is defined as a matrix containing the integers from 1 to n^2 where each row, column, and the two diagonals all have the same sum. This sum, called the magic constant (M), is determined solely by n by this formula:  For the 3x3 square it is 15.

In Matlab, the command "magic(n)" generates a magic matrix when "n" is a scalar larger than or equal to 3.

For example,


>> X=magic(3)

X =

     8     1     6
     3     5     7
     4     9     2

To verify that X is indeed a magic square, I check the sums of its rows, columns, and diagonal:

>> sum(X)

ans =

    15    15    15

>> sum(X')'

ans =

    15

    15

    15

>> sum(diag(X))

ans =

    15

Tada! We have a magic square of order 3!

But how are such magic squares constructed? 

In the spirit of learning the in-and-outs of Matlab, I've been attempting to write an original program that constructs the 3x3 magic square. 

Be back with details on that soon!